| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Section A | Section B | Section C |
| Section D | ||
Class 9th Mathematics Sample Paper Set II (NCERT Exemplar)
Welcome to this crucial section featuring meticulously designed Sample Papers accompanied by their comprehensive solutions, specifically tailored for Class 9 students preparing for examinations that emphasize conceptual depth and application skills. These sample papers are far more than simple practice sets; they are constructed with the express purpose of providing a truly realistic assessment experience. Every effort has been made to mirror the anticipated difficulty level, the diverse typology of questions (ranging from objective to subjective), and the proportional chapter weightage that students are likely to encounter in final assessments, particularly those incorporating Higher-Order Thinking Skills (HOTS) and application-based problems characteristic of the demanding NCERT Exemplar series.
Accompanying each sample paper is a dedicated solutions page, offering complete, step-by-step answers and thorough explanations for every single question presented. This holistic support covers all formats you might face, ensuring no aspect of potential examination structure is overlooked:
- Multiple Choice Questions (MCQs)
- Fill-in-the-Blanks
- True/False statements
- Very Short Answer (VSA) questions
- Short Answer (SA) questions
- Long Answer (LA) questions
These papers draw problems from the entire Class 9 mathematics syllabus, reflecting the breadth and depth explored in the preceding NCERT Exemplar chapters. You will find questions testing your understanding across diverse areas including Number Systems, Polynomials, Coordinate Geometry, Linear Equations in Two Variables, Introduction to Euclid's Geometry, Lines and Angles, Triangles, Quadrilaterals, theorems related to Areas of Parallelograms and Triangles (like $\text{ar}(\triangle) = \frac{1}{2} \text{ar}(\text{gm})$ on the same base and between same parallels), Circles, Constructions, Heron's Formula (Area $= \sqrt{s(s-a)(s-b)(s-c)}$ where $s = \frac{a+b+c}{2}$), Surface Areas and Volumes, Statistics, and Probability.
The provided solutions go beyond just giving the final answer. They serve as a significant learning tool by explicitly demonstrating the practical application of core concepts, formulas, geometric theorems, and effective problem-solving strategies necessary to successfully navigate the varied challenges within each paper. Furthermore, these solutions often highlight how different mathematical topics might be cleverly integrated within a single complex question, offering valuable insights into the interconnectedness of the syllabus. They implicitly guide students on aspects of time management during exams and model the expected standards for clear and logical answer presentation, showing how to structure proofs or calculations systematically.
By diligently working through these sample papers and then critically reviewing the detailed solutions, students gain a powerful mechanism for self-assessment. This process allows you to effectively assess your preparation level across the entire curriculum, pinpoint specific areas or topics requiring further attention and practice, and become comfortable with the expected standard of questions, especially those reflecting the Exemplar's focus on application and higher-order thinking. Practicing under simulated exam conditions helps build confidence, while studying the solutions enables refinement of problem-solving techniques and answer-writing strategies. Ultimately, these solved sample papers stand as invaluable resources for final revision cycles, ensuring comprehensive and targeted preparation for your Class 9 examinations.
Section A
In Questions 1 to 10, four options of answer are given in each, out of which only one is correct. Write the correct option.
Question 1. Which of the following represent a line parallel to x-axis?
(A) x + y = 3
(B) 2x + 3 = 7
(C) 2y − 3 = y +1
(D) x + 3 = 0
Answer:
A line parallel to the x-axis is represented by an equation of the form $y = c$, where $c$ is a constant.
Let's examine each option:
(A) $x + y = 3$. Rearranging this equation, we get $y = -x + 3$. This is in the form $y = mx + c$ with slope $m = -1$, which represents a line that is not parallel to either the x-axis or the y-axis (unless $m=0$ or $m$ is undefined, respectively).
(B) $2x + 3 = 7$. Solving for $x$, we get $2x = 7 - 3 \implies 2x = 4 \implies x = 2$. This is in the form $x = c$, where $c = 2$. A line of this form is parallel to the y-axis.
(C) $2y - 3 = y + 1$. Rearranging this equation to isolate $y$: $2y - y = 1 + 3$ $y = 4$ This is in the form $y = c$, where $c = 4$. A line of this form is parallel to the x-axis.
(D) $x + 3 = 0$. Solving for $x$, we get $x = -3$. This is in the form $x = c$, where $c = -3$. A line of this form is parallel to the y-axis.
From the analysis above, only option (C) results in an equation of the form $y = \text{constant}$, which represents a line parallel to the x-axis.
The correct option is (C).
Question 2. Zero of the polynomial p( x) = 3x + 5 is :
(A) 0
(B) - 5
(C) $\frac{5}{3}$
(D) $\frac{-5}{3}$
Answer:
To find the zero of the polynomial $p(x)$, we set $p(x) = 0$.
Given polynomial is $p(x) = 3x + 5$.
Setting $p(x) = 0$, we get:
$3x + 5 = 0$
... (i)
Now, we solve equation (i) for $x$:
$3x = -5$
$x = \frac{-5}{3}$
Thus, the zero of the polynomial $p(x) = 3x + 5$ is $x = \frac{-5}{3}$.
Comparing this with the given options, the correct option is (D).
Question 3. The abscissa of a point P, in cartesian plane, is the perpendicular distance of P from:
(A) y-axis
(B) x-axis
(C) origin
(D) line y = x
Answer:
In a Cartesian plane, a point P is represented by coordinates $(x, y)$.
The abscissa of the point P is the x-coordinate ($x$).
The abscissa represents the perpendicular distance of the point P from the y-axis.
The ordinate of the point P is the y-coordinate ($y$), which represents the perpendicular distance of the point P from the x-axis.
Therefore, the abscissa of a point P is the perpendicular distance of P from the y-axis.
The correct option is (A).
Question 4. The reflex angle is an angle:
(A) less than 90°
(B) greater than 90°
(C) less than 180°
(D) greater than 180°
Answer:
An angle is classified based on its measure.
Here are some common types of angles:
- An acute angle has a measure between $0^\circ$ and $90^\circ$ ($0^\circ < \text{angle} < 90^\circ$).
- A right angle has a measure of exactly $90^\circ$.
- An obtuse angle has a measure between $90^\circ$ and $180^\circ$ ($90^\circ < \text{angle} < 180^\circ$).
- A straight angle has a measure of exactly $180^\circ$.
- A reflex angle has a measure greater than $180^\circ$ but less than $360^\circ$ ($180^\circ < \text{angle} < 360^\circ$).
- A full angle or complete angle has a measure of exactly $360^\circ$.
Based on these definitions, a reflex angle is an angle that is greater than $180^\circ$.
Comparing this with the given options, the correct option is (D).
Question 5. If the lines l, m, and n are such that l ||m and m||n, then
(A) l || n
(B) l ⊥ n
(C) l and n are intersecting
(D) l = n
Answer:
This question is based on a fundamental property of parallel lines.
The property states that if two distinct lines are both parallel to the same line, then they are parallel to each other.
Given that line l is parallel to line m ($l \ || \ m$).
Also, given that line m is parallel to line n ($m \ || \ n$).
According to the transitive property of parallel lines, since both line l and line n are parallel to the same line m, line l must be parallel to line n.
If $l \ || \ m$ and $m \ || \ n$
Then $l \ || \ n$
Therefore, line l is parallel to line n.
Comparing this conclusion with the given options, the correct option is (A).
Question 6. In Fig.1, B < A and D > C, then:
(A) AD > BC
(B) AD = BC
(C) AD < BC
(D) AD = 2BC

Answer:
Given:
In convex quadrilateral ABCD (as shown in Fig.1):
$\angle B < \angle A$
$\angle D > \angle C$
From the given inequalities, we can write:
$\angle A - \angle B > 0$
$\angle D - \angle C > 0$
Adding these two inequalities:
$(\angle A - \angle B) + (\angle D - \angle C) > 0$
$\angle A + \angle D - \angle B - \angle C > 0$
Rearranging the terms, we get:
$\angle A + \angle D > \angle B + \angle C$
We use a geometric theorem that relates the lengths of opposite sides of a convex quadrilateral to the sums of its adjacent interior angles.
Theorem: In a convex quadrilateral ABCD, the side AD is shorter than the side BC if and only if the sum of the interior angles at vertices B and C is less than the sum of the interior angles at vertices A and D.
That is, $AD < BC \iff \angle B + \angle C < \angle A + \angle D$.
Since we have derived that $\angle B + \angle C < \angle A + \angle D$, according to the theorem, it must be that $AD < BC$.
Therefore, $AD < BC$.
The correct option is (C).
Question 7. In Fig. 2, the measure of ∠BCD is:

(A) 100°
(B) 70°
(C) 80°
(D) 30°
Answer:
Given:
A cyclic quadrilateral ABCD is shown in Fig. 2.
$\angle DAB = 100^\circ$
$\angle ABC = 70^\circ$
To Find:
The measure of $\angle BCD$.
Solution:
We know that the sum of opposite angles in a cyclic quadrilateral is $180^\circ$.
In cyclic quadrilateral ABCD, the pair of opposite angles are $(\angle DAB, \angle BCD)$ and $(\angle ABC, \angle ADC)$.
Therefore, we have:
$\angle DAB + \angle BCD = 180^\circ$
(Sum of opposite angles in a cyclic quadrilateral)
Substitute the given value of $\angle DAB$ into the equation:
$100^\circ + \angle BCD = 180^\circ$
Now, solve for $\angle BCD$:
$\angle BCD = 180^\circ - 100^\circ$
$\angle BCD = 80^\circ$
Thus, the measure of $\angle BCD$ is $80^\circ$.
Comparing this result with the given options, the correct option is (C).
Question 8. The height of a cone of diameter 10 cm and slant height 13cm is:
(A) $\sqrt{69}$
(B) 12 cm
(C) 13 cm
(D) $\sqrt{194}$ cm
Answer:
Given:
Diameter of the cone ($d$) = 10 cm
Slant height of the cone ($l$) = 13 cm
To Find:
The height of the cone ($h$).
Solution:
The radius of the cone ($r$) is half of the diameter.
$r = \frac{d}{2}$
$r = \frac{10}{2} \text{ cm}$
$r = 5 \text{ cm}$
The height ($h$), radius ($r$), and slant height ($l$) of a cone form a right-angled triangle, with the slant height as the hypotenuse. Their relationship is given by the Pythagorean theorem:
$l^2 = r^2 + h^2$
... (i)
Substitute the given values of $l$ and $r$ into equation (i):
$(13)^2 = (5)^2 + h^2$
$169 = 25 + h^2$
Solve for $h^2$:
$h^2 = 169 - 25$
$h^2 = 144$
Take the square root of both sides to find $h$:
$h = \sqrt{144}$
$h = 12 \text{ cm}$
The height of the cone is 12 cm.
Comparing this result with the given options, the correct option is (B).
Question 9. The surface area of a solid hemisphere with radius r is
(A) 4πr2
(B) 2πr2
(C) 3πr2
(D) $\frac{2}{3}$ πr3
Answer:
Given:
A solid hemisphere with radius $r$.
To Find:
The surface area of the solid hemisphere.
Solution:
A solid hemisphere consists of two parts: the curved surface and the flat circular base.
The curved surface area of a hemisphere is half the surface area of a full sphere.
Surface area of a sphere with radius $r = 4\pi r^2$.
Curved surface area of hemisphere $= \frac{1}{2} \times (4\pi r^2) = 2\pi r^2$.
The base of the solid hemisphere is a circle with radius $r$.
Area of the circular base $= \pi r^2$.
The total surface area of a solid hemisphere is the sum of its curved surface area and the area of its base.
Total surface area = Curved surface area + Area of base
Total surface area $= 2\pi r^2 + \pi r^2$
Total surface area $= 3\pi r^2$
Therefore, the surface area of a solid hemisphere with radius $r$ is $3\pi r^2$.
Comparing this result with the given options, the correct option is (C).
Question 10. If the mode of the following data
| 10 | 11 | 12 | 10 | 15 | 14 | 15 | 13 | 12 | $x$ |
| 9 | 7 |
is 15, then the value of x is:
(A) 10
(B) 15
(C) 12
(D) $\frac{21}{2}$
Answer:
Given:
Data set: 10, 11, 12, 10, 15, 14, 15, 13, 12, $x$, 9, 7
Mode of the data = 15
To Find:
The value of $x$.
Solution:
The mode of a data set is the value that appears most frequently.
Let's count the frequency of each number in the given data, excluding $x$ initially:
- 7: 1 time
- 9: 1 time
- 10: 2 times
- 11: 1 time
- 12: 2 times
- 13: 1 time
- 14: 1 time
- 15: 2 times
Currently, the numbers 10, 12, and 15 all appear 2 times, which is the highest frequency among the listed numbers.
The problem states that the mode of the entire data set (including $x$) is 15.
For 15 to be the mode, its frequency must be greater than the frequency of any other number in the data set.
Consider the possibilities for the value of $x$:
If $x = 10$, the frequency of 10 becomes 3, while the frequency of 15 remains 2. The mode would be 10, which contradicts the given information.
If $x = 12$, the frequency of 12 becomes 3, while the frequency of 15 remains 2. The mode would be 12, which contradicts the given information.
If $x = 15$, the frequency of 15 becomes $2+1=3$. The frequencies of 10 and 12 remain 2. The frequency of 15 (which is 3) is now the highest frequency. In this case, the mode is 15, which matches the given information.
If $x$ is equal to any other value that already appears only once (7, 9, 11, 13, or 14), the frequency of that value increases to 2. The highest frequency among all numbers would still be 2 (shared by 10, 12, 15, and the value of $x$), meaning the mode would not be uniquely 15.
If $x$ is equal to a new value (not in the list), its frequency would be 1. The highest frequency would still be 2 (shared by 10, 12, and 15), meaning the mode would not be uniquely 15.
Therefore, the only value of $x$ that makes the mode of the data set equal to 15 is $x = 15$.
The correct option is (B).
Section B
Question 11. Find an irrational number between two numbers $\frac{1}{7}$ and $\frac{2}{7}$ and justify your answer.
It is given that $\frac{1}{7}$ = 0.$\overline{142857}$
Answer:
Given:
Two numbers $\frac{1}{7}$ and $\frac{2}{7}$.
The decimal expansion of $\frac{1}{7}$ is given as $0.\overline{142857}$.
To Find:
An irrational number between $\frac{1}{7}$ and $\frac{2}{7}$ and to justify the answer.
Solution:
First, let's find the decimal expansion of $\frac{2}{7}$.
$\frac{2}{7} = 2 \times \frac{1}{7}$
$\frac{2}{7} = 2 \times 0.\overline{142857}$
$\frac{2}{7} = 0.\overline{285714}$
So, we need to find an irrational number between $0.\overline{142857}$ and $0.\overline{285714}$.
An irrational number is a number that cannot be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$. In decimal form, an irrational number is non-terminating and non-repeating.
We need to find a number whose decimal expansion is non-terminating and non-repeating, and lies between $0.142857...$ and $0.285714...$.
We can choose a number whose decimal expansion starts with digits that fall between 142857 and 285714, and then add a pattern of digits that does not repeat.
For example, consider the number $0.1501001000100001...$.
Justification:
This number is between $\frac{1}{7}$ and $\frac{2}{7}$ because:
The first digit after the decimal point is 1 in both $0.\overline{142857}$ and $0.1501...$. The second digit is 4 in $0.\overline{142857}$ and 5 in $0.1501...$. Since $5 > 4$, we have $0.1501001000100001... > 0.\overline{142857}$.
The first digit after the decimal point is 1 in $0.1501...$ and 2 in $0.\overline{285714}$. Since $1 < 2$, we have $0.1501001000100001... < 0.\overline{285714}$.
Thus, the number $0.1501001000100001...$ lies between $0.\overline{142857}$ and $0.\overline{285714}$.
The number $0.1501001000100001...$ is irrational because its decimal expansion is non-terminating (it goes on infinitely) and non-repeating (the pattern of zeros between the ones increases: one zero, then two zeros, then three zeros, and so on, ensuring no block of digits repeats periodically).
Therefore, an irrational number between $\frac{1}{7}$ and $\frac{2}{7}$ is $0.1501001000100001...$ (or any other similarly constructed non-terminating, non-repeating decimal between $0.\overline{142857}$ and $0.\overline{285714}$).
Question 12. Without actually dividing, find the remainder when x4 + x3 − 2x2 + x +1 is divided by x −1, and justify your answer.
Answer:
Given:
Polynomial $p(x) = x^4 + x^3 - 2x^2 + x + 1$
Divisor $g(x) = x - 1$
To Find:
The remainder when $p(x)$ is divided by $g(x)$, without actual division.
Solution:
We can use the **Remainder Theorem** to find the remainder without performing long division.
Remainder Theorem:
When a polynomial $p(x)$ is divided by a linear polynomial $x-a$, the remainder is $p(a)$.
In this case, the polynomial is $p(x) = x^4 + x^3 - 2x^2 + x + 1$, and the divisor is $x - 1$.
Comparing the divisor $x - 1$ with the general form $x - a$, we find that $a = 1$.
According to the Remainder Theorem, the remainder is $p(1)$.
Let's evaluate $p(1)$ by substituting $x = 1$ into the polynomial:
$p(1) = (1)^4 + (1)^3 - 2(1)^2 + (1) + 1$
$p(1) = 1 + 1 - 2(1) + 1 + 1$
$p(1) = 1 + 1 - 2 + 1 + 1$
$p(1) = (1 + 1 + 1 + 1) - 2$
$p(1) = 4 - 2$
$p(1) = 2$
The remainder when $x^4 + x^3 - 2x^2 + x + 1$ is divided by $x - 1$ is 2.
Justification:
Our answer is justified by the **Remainder Theorem**, which states that for any polynomial $p(x)$ and any number $a$, the remainder on division by $x-a$ is $p(a)$. In this specific case, dividing by $x-1$ means $a=1$, and the remainder is $p(1)$. We calculated $p(1)$ to be 2, which is the remainder according to the theorem.
Question 13. Give the equations of two lines passing through (2, 10). How many more such lines are there, and why?
Answer:
Given:
A point with coordinates (2, 10).
To Find:
Equations of two lines passing through the point (2, 10). The number of such lines and justification.
Solution:
A linear equation in two variables, say $ax + by = c$, represents a line in the Cartesian plane. A point $(x_0, y_0)$ lies on the line if its coordinates satisfy the equation, i.e., $ax_0 + by_0 = c$.
For the point (2, 10), we need to find equations $ax + by = c$ such that $a(2) + b(10) = c$.
We can choose different values for $a$ and $b$ (not both zero) to find corresponding values of $c$ and thus different equations.
First Equation:
Let $a=1$ and $b=1$. Then $c = 1(2) + 1(10) = 2 + 10 = 12$.
The equation of the line is $x + y = 12$.
Check: $2 + 10 = 12$. The point (2, 10) satisfies the equation.
Second Equation:
Let $a=5$ and $b=-1$. Then $c = 5(2) + (-1)(10) = 10 - 10 = 0$.
The equation of the line is $5x - y = 0$ or $y = 5x$.
Check: $5(2) - 10 = 10 - 10 = 0$. The point (2, 10) satisfies the equation.
So, two equations of lines passing through (2, 10) are:
$x + y = 12$
and
$y = 5x$
Number of such lines:
There are **infinitely many** more such lines.
Justification:
A fundamental geometric postulate states that **through a single point, infinitely many lines can pass**. This is because a line is determined by two distinct points or by one point and a slope. If we fix one point (2, 10), we can draw a line through this point with any possible slope.
Consider the general equation of a non-vertical line $y = mx + c$. Since the point (2, 10) lies on the line, it must satisfy the equation:
$10 = m(2) + c$
From this, we can express $c$ in terms of $m$:
$c = 10 - 2m$
Substituting this back into the general equation, we get the equation of any non-vertical line passing through (2, 10):
$y = mx + (10 - 2m)$
Since $m$ can be any real number, there are infinitely many possible values for $m$. Each distinct value of $m$ gives a unique line passing through (2, 10).
Additionally, there is the vertical line passing through (2, 10), which has the equation $x = 2$. This line cannot be represented in the form $y = mx + c$.
Combining the infinitely many non-vertical lines (one for each real value of $m$) and the single vertical line, we conclude that there are **infinitely many** lines passing through the point (2, 10).
Question 14. Two points with coordinates (2, 3) and (2, –1) lie on a line, parallel to which axis? Justify your answer.
Answer:
Given:
Two points with coordinates (2, 3) and (2, -1).
To Find:
The axis to which the line passing through the given points is parallel, and justification.
Solution:
Let the two given points be P(2, 3) and Q(2, -1).
Observe the coordinates of the two points. The x-coordinate is the same for both points (it is 2).
If two points have the same x-coordinate, the line passing through them is a vertical line.
The equation of a vertical line passing through a point $(c, y)$ is $x = c$.
Since both points have an x-coordinate of 2, the equation of the line passing through (2, 3) and (2, -1) is $x = 2$.
A line with the equation $x = c$ is a vertical line, which is parallel to the y-axis.
Therefore, the line passing through the points (2, 3) and (2, -1) is parallel to the y-axis.
Justification:
The equation of any line can be written in the form $Ax + By + C = 0$. If a line is parallel to the y-axis, its equation must be of the form $x = c$, or $x - c = 0$, which means $A=1$, $B=0$, and $C=-c$. This form indicates that the y-coordinate can vary freely while the x-coordinate remains constant.
Alternatively, consider the slope of the line passing through the points $(x_1, y_1)$ and $(x_2, y_2)$. The slope ($m$) is given by:
$m = \frac{y_2 - y_1}{x_2 - x_1}$
For the points (2, 3) and (2, -1):
$x_1 = 2, y_1 = 3$
$x_2 = 2, y_2 = -1$
Calculating the slope:
$m = \frac{-1 - 3}{2 - 2}$
$m = \frac{-4}{0}$
Since division by zero is undefined, the slope of the line is undefined. Lines with undefined slope are vertical lines.
Vertical lines are parallel to the y-axis.
This justifies that the line passing through (2, 3) and (2, -1) is parallel to the y-axis because all points on the line share the same x-coordinate, resulting in an undefined slope.
Question 15. A die was rolled 100 times and the number of times, 6 came up was noted. If the experimental probability calculated from this information is $\frac{2}{5}$ then how many times 6 came up? Justify your answer.
Answer:
Given:
Total number of times the die was rolled (Total trials) = 100.
Experimental probability of getting a 6 = $\frac{2}{5}$.
To Find:
The number of times 6 came up.
Solution:
Let the number of times 6 came up be $n_6$.
The formula for experimental probability is:
Experimental Probability = $\frac{\text{Number of times the event occurred}}{\text{Total number of trials}}$
In this case, the event is getting a 6. So, the experimental probability of getting a 6 is:
$P(\text{getting a 6}) = \frac{n_6}{100}$
We are given that the experimental probability of getting a 6 is $\frac{2}{5}$.
Therefore, we can set up the equation:
$\frac{n_6}{100} = \frac{2}{5}$
... (i)
Now, we solve equation (i) for $n_6$:
$n_6 = \frac{2}{5} \times 100$
$n_6 = 2 \times \frac{\cancel{100}^{20}}{\cancel{5}_{1}}$
$n_6 = 2 \times 20$
$n_6 = 40$
So, the number of times 6 came up is 40.
Justification:
We used the definition of experimental probability. If 6 came up 40 times in 100 rolls, the experimental probability is calculated as:
Experimental Probability = $\frac{40}{100}$
Simplifying the fraction:
$\frac{40}{100} = \frac{\cancel{40}^{2}}{\cancel{100}_{5}} = \frac{2}{5}$
This calculated probability $\frac{2}{5}$ matches the given experimental probability. Thus, our answer is justified.
Section C
Question 16. Find three rational numbers between $\frac{2}{5}$ and $\frac{3}{5}$
Answer:
Given:
Two rational numbers $\frac{2}{5}$ and $\frac{3}{5}$.
To Find:
Three rational numbers between $\frac{2}{5}$ and $\frac{3}{5}$.
Solution:
To find rational numbers between two given rational numbers, we can express them with a common denominator. To find multiple numbers, we can multiply both the numerator and the denominator of the given fractions by a factor greater than the number of rational numbers we want to find plus one. Since we need 3 rational numbers, let's multiply by $3+1=4$ (or any number greater than 4).
Let's multiply both the numerator and the denominator of $\frac{2}{5}$ and $\frac{3}{5}$ by 10 (any integer greater than 1 would work, but 10 is convenient for decimal comparison):
$\frac{2}{5} = \frac{2 \times 10}{5 \times 10} = \frac{20}{50}$
$\frac{3}{5} = \frac{3 \times 10}{5 \times 10} = \frac{30}{50}$
Now we need to find three rational numbers between $\frac{20}{50}$ and $\frac{30}{50}$.
The integers between 20 and 30 are 21, 22, 23, 24, 25, 26, 27, 28, and 29.
We can form rational numbers by using these integers as numerators and keeping the denominator as 50.
Three rational numbers between $\frac{20}{50}$ and $\frac{30}{50}$ are, for example, $\frac{21}{50}$, $\frac{22}{50}$, and $\frac{23}{50}$.
We can simplify these fractions if possible. $\frac{21}{50}$ cannot be simplified. $\frac{22}{50}$ can be simplified to $\frac{11}{25}$. $\frac{23}{50}$ cannot be simplified.
Alternatively, we can use decimal form. $\frac{2}{5} = 0.4$ and $\frac{3}{5} = 0.6$.
We need to find three rational numbers between 0.4 and 0.6.
Rational numbers between 0.4 and 0.6 are, for example, 0.41, 0.42, 0.5, 0.55, etc.
These can be written as fractions:
$0.41 = \frac{41}{100}$
$0.42 = \frac{42}{100} = \frac{21}{50}$
$0.5 = \frac{5}{10} = \frac{1}{2}$
Any three rational numbers between $\frac{20}{50}$ and $\frac{30}{50}$ (exclusive) are valid answers.
Three rational numbers between $\frac{2}{5}$ and $\frac{3}{5}$ are $\frac{21}{50}$, $\frac{22}{50}$ (or $\frac{11}{25}$), and $\frac{23}{50}$.
Question 17. Factorise: 54a3 - 250b3
Answer:
Given Expression:
$54a^3 - 250b^3$
To Factorise:
Factorise the given expression.
Solution:
First, we look for a common factor in the two terms $54a^3$ and $250b^3$.
The prime factorisation of 54 is $2 \times 3 \times 3 \times 3 = 2 \times 3^3$.
The prime factorisation of 250 is $2 \times 5 \times 5 \times 5 = 2 \times 5^3$.
The common factor is 2.
We can factor out 2 from both terms:
$54a^3 - 250b^3 = 2(27a^3 - 125b^3)$
Now, we need to factorise the expression inside the parenthesis, $27a^3 - 125b^3$.
Notice that $27a^3 = (3a)^3$ and $125b^3 = (5b)^3$.
The expression is in the form of the difference of cubes, $X^3 - Y^3$, where $X = 3a$ and $Y = 5b$.
The formula for the difference of cubes is:
$X^3 - Y^3 = (X - Y)(X^2 + XY + Y^2)$
... (i)
Using this formula with $X = 3a$ and $Y = 5b$, we can factorise $27a^3 - 125b^3$:
$(3a)^3 - (5b)^3 = (3a - 5b)((3a)^2 + (3a)(5b) + (5b)^2)$
$= (3a - 5b)(9a^2 + 15ab + 25b^2)$
Substitute this back into the original expression after factoring out 2:
$54a^3 - 250b^3 = 2(27a^3 - 125b^3)$
$= 2(3a - 5b)(9a^2 + 15ab + 25b^2)$
The factorisation of $54a^3 - 250b^3$ is $2(3a - 5b)(9a^2 + 15ab + 25b^2)$.
Question 18. Check whether the polynomial
p(y) = 2y3 + y2 +4y −15 is a multiple of (2y – 3).
Answer:
Given:
Polynomial $p(y) = 2y^3 + y^2 + 4y - 15$
Divisor $g(y) = 2y - 3$
To Check:
Whether $p(y)$ is a multiple of $(2y - 3)$.
Solution:
A polynomial $p(y)$ is a multiple of another polynomial $g(y)$ if and only if the remainder when $p(y)$ is divided by $g(y)$ is 0.
We can use the Remainder Theorem to find the remainder without actual division.
Remainder Theorem:
When a polynomial $p(y)$ is divided by a linear polynomial $(y-a)$, the remainder is $p(a)$.
The divisor is $2y - 3$. To use the Remainder Theorem in the form $(y-a)$, we set the divisor equal to zero and solve for $y$:
$2y - 3 = 0$
$2y = 3$
$y = \frac{3}{2}$
According to the Remainder Theorem, the remainder when $p(y)$ is divided by $(2y - 3)$ (or effectively by $(y - \frac{3}{2})$) is $p(\frac{3}{2})$.
Substitute $y = \frac{3}{2}$ into the polynomial $p(y)$:
$p(\frac{3}{2}) = 2(\frac{3}{2})^3 + (\frac{3}{2})^2 + 4(\frac{3}{2}) - 15$
$p(\frac{3}{2}) = 2(\frac{3^3}{2^3}) + (\frac{3^2}{2^2}) + \frac{4 \times 3}{2} - 15$
$p(\frac{3}{2}) = 2(\frac{27}{8}) + \frac{9}{4} + \frac{12}{2} - 15$
$p(\frac{3}{2}) = \frac{2 \times 27}{8} + \frac{9}{4} + 6 - 15$
$p(\frac{3}{2}) = \frac{54}{8} + \frac{9}{4} + 6 - 15$
$p(\frac{3}{2}) = \frac{27}{4} + \frac{9}{4} + 6 - 15$
Combine the fractions with the same denominator:
$p(\frac{3}{2}) = \frac{27 + 9}{4} + 6 - 15$
$p(\frac{3}{2}) = \frac{36}{4} + 6 - 15$
$p(\frac{3}{2}) = 9 + 6 - 15$
$p(\frac{3}{2}) = 15 - 15$
$p(\frac{3}{2}) = 0$
Since the remainder is 0 when $p(y)$ is evaluated at $y = \frac{3}{2}$, which is the zero of the divisor $2y - 3$, by the Remainder Theorem, the remainder of the division of $p(y)$ by $(2y - 3)$ is 0.
A polynomial is a multiple of another polynomial if the remainder upon division is zero.
Since the remainder is 0, the polynomial $p(y) = 2y^3 + y^2 + 4y - 15$ is a multiple of $(2y - 3)$.
Answer:
Yes, the polynomial $p(y) = 2y^3 + y^2 + 4y - 15$ is a multiple of $(2y - 3)$.
Question 19. If the point (3, 4) lies on the graph of the equation 2y = ax + 6 , find whether (6, 5) also lies on the same graph.
Answer:
Given:
The equation of a line is $2y = ax + 6$.
The point (3, 4) lies on the graph of this equation.
To Find:
Whether the point (6, 5) also lies on the same graph.
Solution:
Since the point (3, 4) lies on the graph of the equation $2y = ax + 6$, its coordinates must satisfy the equation.
Substitute $x = 3$ and $y = 4$ into the equation:
$2(4) = a(3) + 6$
$8 = 3a + 6$
Now, solve for the value of $a$:
$8 - 6 = 3a$
$2 = 3a$
$a = \frac{2}{3}$
Substitute the value of $a = \frac{2}{3}$ back into the original equation to get the specific equation of the line:
$2y = \frac{2}{3}x + 6$
... (i)
Now, we need to check if the point (6, 5) lies on the graph of equation (i). A point lies on the graph if its coordinates satisfy the equation.
Substitute $x = 6$ and $y = 5$ into equation (i):
$2(5) = \frac{2}{3}(6) + 6$
$10 = \frac{2 \times \cancel{6}^{2}}{\cancel{3}_{1}} + 6$
$10 = 2 \times 2 + 6$
$10 = 4 + 6$
$10 = 10$
Since the equation is satisfied when $x=6$ and $y=5$, the point (6, 5) lies on the graph of the equation $2y = \frac{2}{3}x + 6$.
Answer:
Yes, the point (6, 5) also lies on the same graph.
Question 20. Plot (–3, 0), (5, 0) and (0, 4) on cartesian plane. Name the figure formed by joining these points and find its area.
Answer:
Given:
The points A(–3, 0), B(5, 0), and C(0, 4).
To Find:
Name the figure formed by joining the points and find its area.
Solution:
Let the points be A(–3, 0), B(5, 0), and C(0, 4).
When these three non-collinear points are joined by line segments, the figure formed is a **triangle**.
To find the area of the triangle ABC, we can use the coordinates of its vertices.
Observe that points A(–3, 0) and B(5, 0) lie on the x-axis because their y-coordinates are 0.
The distance between these two points can be taken as the base of the triangle.
Length of the base AB = distance between A(–3, 0) and B(5, 0).
Length of base AB = $|5 - (-3)|$
Length of base AB = $|5 + 3|$
Length of base AB = $|8|$
Base = 8 units
The height of the triangle with base AB (lying on the x-axis) is the perpendicular distance from the vertex C(0, 4) to the x-axis.
The perpendicular distance of a point $(x, y)$ from the x-axis is $|y|$.
Height of the triangle = perpendicular distance of C(0, 4) from the x-axis.
Height = $|4|$
Height = 4 units
The area of a triangle is given by the formula:
Area $= \frac{1}{2} \times \text{base} \times \text{height}$
Substitute the values of base and height:
Area $= \frac{1}{2} \times 8 \times 4$
Area $= \frac{1}{2} \times 32$
Area $= 16$
The figure formed by joining the points A(–3, 0), B(5, 0), and C(0, 4) is a triangle.
The area of the triangle is 16 square units.
Question 21. Diagonals AC and BD of a trapezium ABCD with AB DC, intersect each other at O. Prove that ar(AOD) = ar(BOC).
OR
ABCD is a rectangle in which diagonal AC bisects A as well as C. Show that ABCD is a square.
Answer:
We will solve the first part of the question.
Given:
ABCD is a trapezium.
AB || DC.
Diagonals AC and BD intersect at O.
To Prove:
ar(AOD) = ar(BOC).
Proof:
Consider the triangles $\triangle$ABD and $\triangle$ABC.
These two triangles are on the same base AB and between the same parallel lines AB and DC.
We know that triangles on the same base and between the same parallels have equal areas.
ar($\triangle$ ABD) = ar($\triangle$ ABC)
(Triangles on the same base AB and between same parallels AB and DC)
Now, subtract the area of the common triangle $\triangle$AOB from both sides of the equation:
ar($\triangle$ ABD) - ar($\triangle$ AOB) = ar($\triangle$ ABC) - ar($\triangle$ AOB)
Observe the areas on the left side and the right side of the equation from the figure:
ar($\triangle$ ABD) - ar($\triangle$ AOB) = ar($\triangle$ AOD)
and
ar($\triangle$ ABC) - ar($\triangle$ AOB) = ar($\triangle$ BOC)
Substituting these back into the subtracted equation, we get:
ar($\triangle$ AOD) = ar($\triangle$ BOC)
Thus, the area of triangle AOD is equal to the area of triangle BOC.
Hence Proved.
Alternate Solution (for the "OR" part):
Given:
ABCD is a rectangle.
Diagonal AC bisects $\angle A$ and $\angle C$.
To Show:
ABCD is a square.
Proof:
Since ABCD is a rectangle, all its interior angles are $90^\circ$.
$\angle A = \angle B = \angle C = \angle D = 90^\circ$
(Angles of a rectangle)
Given that the diagonal AC bisects $\angle A$, it divides $\angle A$ into two equal angles:
$\angle BAC = \angle DAC = \frac{1}{2} \angle A$
(AC bisects $\angle$A)
$\angle BAC = \angle DAC = \frac{1}{2} \times 90^\circ = 45^\circ$
Given that the diagonal AC also bisects $\angle C$, it divides $\angle C$ into two equal angles:
$\angle BCA = \angle DCA = \frac{1}{2} \angle C$
(AC bisects $\angle$C)
$\angle BCA = \angle DCA = \frac{1}{2} \times 90^\circ = 45^\circ$
Now, consider $\triangle ABC$.
We have $\angle BAC = 45^\circ$ and $\angle BCA = 45^\circ$.
$\angle BAC = \angle BCA$
In a triangle, sides opposite to equal angles are equal.
BC = AB
(Sides opposite to equal angles in $\triangle$ABC)
Since ABCD is a rectangle, its opposite sides are equal:
AB = DC
(Opposite sides of a rectangle)
BC = AD
(Opposite sides of a rectangle)
Combining the results, we have AB = BC, and we know AB = DC and BC = AD.
Therefore, AB = BC = CD = DA.
A rectangle is a parallelogram with four right angles. If a rectangle has all four sides equal, it is a square.
Since ABCD is a rectangle and its adjacent sides AB and BC are equal (which implies all sides are equal), ABCD is a square.
Hence Proved.
Question 22. Construct a triangle PQR in which Q = 60° and R = 45° and PQ + QR + PR = 11 cm.
Answer:
Given:
In $\triangle PQR$, $\angle Q = 60^\circ$, $\angle R = 45^\circ$, and $PQ + QR + PR = 11$ cm (Perimeter).
To Construct:
Triangle PQR.
Construction Required:
We use the given perimeter and base angles to construct the triangle.
Solution (Steps of Construction):
Step 1: Draw a line segment XY equal to the perimeter of $\triangle PQR$, i.e., $XY = PQ + QR + PR = 11$ cm.
Step 2: At point X, construct an angle equal to half of $\angle Q$. Let's draw $\angle AXY = \frac{1}{2} \times \angle Q = \frac{1}{2} \times 60^\circ = 30^\circ$.
Step 3: At point Y, construct an angle equal to half of $\angle R$. Let's draw $\angle BYX = \frac{1}{2} \times \angle R = \frac{1}{2} \times 45^\circ = 22.5^\circ$. (To construct $22.5^\circ$, bisect the angle $45^\circ$, which is obtained by bisecting $90^\circ$).
Step 4: Let the ray XA and the ray YB intersect each other at point P.
Step 5: Draw the perpendicular bisector of the line segment PX. Let this perpendicular bisector intersect XY at point Q.
Step 6: Draw the perpendicular bisector of the line segment PY. Let this perpendicular bisector intersect XY at point R.
Step 7: Join PQ and PR.
Triangle PQR is the required triangle.
Justification:
By construction, Q lies on the perpendicular bisector of PX. Therefore, any point on the perpendicular bisector of PX is equidistant from P and X.
$PQ = XQ$
In $\triangle PXQ$, since $PQ = XQ$, $\triangle PXQ$ is an isosceles triangle.
$\angle XPQ = \angle PXQ$
(Angles opposite to equal sides)
We constructed $\angle PXQ = \angle AXY = 30^\circ$.
$\angle XPQ = 30^\circ$
The angle $\angle PQR$ is the exterior angle of $\triangle PXQ$ at Q (since Q is on XY). By the exterior angle theorem, the exterior angle is equal to the sum of the two opposite interior angles.
$\angle PQR = \angle PXQ + \angle XPQ$
$\angle PQR = 30^\circ + 30^\circ = 60^\circ$
Thus, $\angle PQR = 60^\circ$, which is the required angle $\angle Q$.
Similarly, R lies on the perpendicular bisector of PY. Therefore,
$PR = YR$
In $\triangle PYR$, since $PR = YR$, $\triangle PYR$ is an isosceles triangle.
$\angle YPR = \angle PYR$
(Angles opposite to equal sides)
We constructed $\angle PYR = \angle BYX = 22.5^\circ$.
$\angle YPR = 22.5^\circ$
The angle $\angle PRQ$ is the exterior angle of $\triangle PYR$ at R (since R is on XY). By the exterior angle theorem,
$\angle PRQ = \angle PYR + \angle YPR$
$\angle PRQ = 22.5^\circ + 22.5^\circ = 45^\circ$
Thus, $\angle PRQ = 45^\circ$, which is the required angle $\angle R$.
Finally, let's check the perimeter of $\triangle PQR$.
Perimeter $= PQ + QR + PR$
Substitute $PQ = XQ$ and $PR = YR$:
Perimeter $= XQ + QR + YR$
From the figure, we can see that $XQ + QR + YR$ is the length of the segment XY (since Q and R are on XY and R is to the right of Q).
Perimeter $= XY$
We constructed XY = 11 cm.
Perimeter $= 11$ cm
The perimeter is 11 cm, which is the required perimeter.
Since $\triangle PQR$ satisfies the given angle measures ($\angle Q = 60^\circ$ and $\angle R = 45^\circ$) and the given perimeter (11 cm), it is the required triangle.
Question 23. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Answer:
Given:
Lengths of two sides of a triangle are $a = 18$ cm and $b = 10$ cm.
The perimeter of the triangle is 42 cm.
To Find:
The area of the triangle.
Solution:
Let the lengths of the three sides of the triangle be $a$, $b$, and $c$.
We are given $a = 18$ cm and $b = 10$ cm.
The perimeter of the triangle is the sum of the lengths of its three sides:
Perimeter $= a + b + c$
We are given Perimeter = 42 cm.
$42 = 18 + 10 + c$
$42 = 28 + c$
Solve for the length of the third side, $c$:
$c = 42 - 28$
$c = 14$ cm
The lengths of the three sides of the triangle are $a = 18$ cm, $b = 10$ cm, and $c = 14$ cm.
To find the area of the triangle given its side lengths, we can use **Heron's formula**.
Heron's Formula:
The area of a triangle with side lengths $a$, $b$, and $c$ is given by $\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$, where $s$ is the semi-perimeter of the triangle.
The semi-perimeter $s$ is half of the perimeter:
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{42}{2}$
$s = 21$ cm
Now, calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$:
$s - a = 21 - 18 = 3$ cm
$s - b = 21 - 10 = 11$ cm
$s - c = 21 - 14 = 7$ cm
Substitute these values into Heron's formula:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Area $= \sqrt{21 \times 3 \times 11 \times 7}$
Factorise the numbers under the square root to simplify:
$21 = 3 \times 7$
Area $= \sqrt{(3 \times 7) \times 3 \times 11 \times 7}$
Area $= \sqrt{3^2 \times 7^2 \times 11}$
Area $= \sqrt{3^2} \times \sqrt{7^2} \times \sqrt{11}$
Area $= 3 \times 7 \times \sqrt{11}$
Area $= 21\sqrt{11}$
The area of the triangle is $21\sqrt{11}$ cm$^2$.
Question 24. A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of Rs 12.50 per m2.
OR
The height of a solid cone is 16 cm and its base radius is 12 cm. Find the total surface area of cone $\left(Use \;\pi = \frac{22}{7} \right)$
Answer:
Solving the "OR" part.
Given: Cone with height $h = 16$ cm and radius $r = 12$ cm.
To Find: Total surface area (TSA).
The slant height $l$ is given by $l = \sqrt{r^2 + h^2}$.
$l = \sqrt{(12)^2 + (16)^2}$
$l = \sqrt{144 + 256}$
$l = \sqrt{400}$
$l = 20$ cm
The total surface area (TSA) of a solid cone is $TSA = \pi r (l + r)$.
$TSA = \frac{22}{7} \times 12 \times (20 + 12)$
$TSA = \frac{22}{7} \times 12 \times 32$
$TSA = \frac{264 \times 32}{7}$
$TSA = \frac{8448}{7}$
The total surface area of the cone is $\frac{8448}{7}$ cm$^2$.
Question 25. A die is thrown 400 times, the frequency of the outcomes of the events are given as under.
| Outcome | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Frequency | 70 | 65 | 60 | 75 | 63 | 67 |
Find the probability of occurence of an odd number.
Answer:
Given:
Total number of times a die is thrown = 400.
Frequencies of outcomes are given in the table:
| Outcome | 1 | 2 | 3 | 4 | 5 | 6 |
| Frequency | 70 | 65 | 60 | 75 | 63 | 67 |
To Find:
The probability of occurrence of an odd number.
Solution:
The total number of trials is 400.
Total trials = 400
We need to find the probability of getting an odd number. The odd outcomes when a die is thrown are 1, 3, and 5.
Let the event of getting an odd number be E.
The frequency of the outcome 1 is 70.
The frequency of the outcome 3 is 60.
The frequency of the outcome 5 is 63.
The number of times an odd number occurred (Number of favorable outcomes for event E) is the sum of the frequencies of 1, 3, and 5.
Number of favorable outcomes = Frequency of 1 + Frequency of 3 + Frequency of 5
Number of favorable outcomes = $70 + 60 + 63$
Number of favorable outcomes = $130 + 63 = 193$
The experimental probability of an event is given by:
$P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of trials}}$
Substitute the values:
$P(\text{getting an odd number}) = \frac{193}{400}$
The probability of occurrence of an odd number is $\frac{193}{400}$.
Section D
Question 26. A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Answer:
Given:
A trapezium with parallel sides $a = 25$ m and $b = 10$ m.
Non-parallel sides are $c = 14$ m and $d = 13$ m.
To Find:
The area of the trapezium.
Solution:
To find the area of a trapezium, we typically need the lengths of the parallel sides and the perpendicular distance between them (the height).
Area of trapezium $= \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$.
Since the height is not directly given, we need to construct the height.
Let the trapezium be ABCD, where AB || DC. Let AB = 25 m and DC = 10 m. Let AD = 14 m and BC = 13 m.
Draw a line CE parallel to AD from C to AB, such that E lies on AB.
Since AD || CE and DC || AE (part of AB), ADCE is a parallelogram.
In a parallelogram, opposite sides are equal.
AE = DC = 10 m
CE = AD = 14 m
Now consider $\triangle$CEB.
The side EB = AB - AE = 25 m - 10 m = 15 m.
The sides of $\triangle$CEB are CE = 14 m, BC = 13 m, and EB = 15 m.
We can find the area of $\triangle$CEB using Heron's formula. Let the sides of $\triangle$CEB be $a' = 13$ m, $b' = 14$ m, and $c' = 15$ m.
The semi-perimeter of $\triangle$CEB is $s' = \frac{a' + b' + c'}{2}$.
$s' = \frac{13 + 14 + 15}{2} = \frac{42}{2} = 21$ m
Using Heron's formula, Area($\triangle$CEB) $= \sqrt{s'(s'-a')(s'-b')(s'-c')}$.
$s' - a' = 21 - 13 = 8$
$s' - b' = 21 - 14 = 7$
$s' - c' = 21 - 15 = 6$
Area($\triangle$CEB) $= \sqrt{21 \times 8 \times 7 \times 6}$
Area($\triangle$CEB) $= \sqrt{(3 \times 7) \times (2^3) \times 7 \times (2 \times 3)}$
Area($\triangle$CEB) $= \sqrt{2^4 \times 3^2 \times 7^2}$
Area($\triangle$CEB) $= \sqrt{(2^2)^2 \times 3^2 \times 7^2}$
Area($\triangle$CEB) $= 2^2 \times 3 \times 7$
Area($\triangle$CEB) $= 4 \times 3 \times 7 = 12 \times 7 = 84 \text{ m}^2$
Now, we can use the area of $\triangle$CEB to find the height of the trapezium. Let $h$ be the height of the trapezium, which is the perpendicular distance from C to AB.
Area($\triangle$CEB) $= \frac{1}{2} \times \text{base EB} \times \text{height } h$
$84 = \frac{1}{2} \times 15 \times h$
Solve for $h$:
$168 = 15h$
$h = \frac{168}{15} = \frac{56}{5} = 11.2$ m
Now that we have the height of the trapezium, we can find its area.
Area of trapezium ABCD $= \frac{1}{2} \times (\text{AB} + \text{DC}) \times h$
Area of trapezium ABCD $= \frac{1}{2} \times (25 \text{ m} + 10 \text{ m}) \times 11.2 \text{ m}$
Area of trapezium ABCD $= \frac{1}{2} \times 35 \text{ m} \times 11.2 \text{ m}$
Area of trapezium ABCD $= 35 \times \frac{11.2}{2} \text{ m}^2$
Area of trapezium ABCD $= 35 \times 5.6 \text{ m}^2$
Area of trapezium ABCD $= 196 \text{ m}^2$
The area of the field is 196 m$^2$.
Question 27. Draw a histogram and frequency polygon for the following distribution:
| Mark Obtained | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 | 70 - 80 |
|---|---|---|---|---|---|---|---|---|
| No. of Students | 7 | 10 | 6 | 8 | 12 | 3 | 2 | 2 |
Answer:
Given:
A frequency distribution table showing the marks obtained by students and the number of students (frequency) for each class interval.
| Mark Obtained (Class Interval) | No. of Students (Frequency) |
| 0 - 10 | 7 |
| 10 - 20 | 10 |
| 20 - 30 | 6 |
| 30 - 40 | 8 |
| 40 - 50 | 12 |
| 50 - 60 | 3 |
| 60 - 70 | 2 |
| 70 - 80 | 2 |
To Draw:
A histogram and a frequency polygon for the given data.
Solution (Steps for Drawing):
We will draw the histogram first, and then use it to draw the frequency polygon.
Steps for Drawing the Histogram:
1. Draw two perpendicular axes on a graph paper. The horizontal axis (x-axis) represents the 'Marks Obtained' and the vertical axis (y-axis) represents the 'No. of Students (Frequency)'.
2. Mark the class boundaries (0, 10, 20, 30, 40, 50, 60, 70, 80) on the x-axis. Since the class intervals are starting from 0 and are continuous, we can start the x-axis from 0.
3. Choose a suitable scale for the y-axis to represent the frequencies. For example, 1 unit length on the y-axis could represent 1 or 2 students.
4. Construct rectangles with the class intervals as bases and the frequencies as heights. For each class interval, draw a rectangle from the lower limit to the upper limit on the x-axis, with a height corresponding to the frequency of that class on the y-axis.
- For 0-10, draw a rectangle of height 7.
- For 10-20, draw a rectangle of height 10.
- For 20-30, draw a rectangle of height 6.
- For 30-40, draw a rectangle of height 8.
- For 40-50, draw a rectangle of height 12.
- For 50-60, draw a rectangle of height 3.
- For 60-70, draw a rectangle of height 2.
- For 70-80, draw a rectangle of height 2.
The rectangles will be adjacent to each other as there are no gaps between the class intervals.
Steps for Drawing the Frequency Polygon (using the Histogram):
1. Find the midpoint of the upper side of each rectangle in the histogram. These midpoints correspond to the class marks. The class mark of an interval is calculated as $\frac{\text{Lower Limit} + \text{Upper Limit}}{2}$.
| Class Interval | Class Mark | Frequency |
| 0 - 10 | $\frac{0+10}{2} = 5$ | 7 |
| 10 - 20 | $\frac{10+20}{2} = 15$ | 10 |
| 20 - 30 | $\frac{20+30}{2} = 25$ | 6 |
| 30 - 40 | $\frac{30+40}{2} = 35$ | 8 |
| 40 - 50 | $\frac{40+50}{2} = 45$ | 12 |
| 50 - 60 | $\frac{50+60}{2} = 55$ | 3 |
| 60 - 70 | $\frac{60+70}{2} = 65$ | 2 |
| 70 - 80 | $\frac{70+80}{2} = 75$ | 2 |
2. Mark these midpoints (5, 7), (15, 10), (25, 6), (35, 8), (45, 12), (55, 3), (65, 2), (75, 2) on the graph.
3. To make the area under the frequency polygon equal to the area under the histogram, we assume there are two imaginary classes, one before the first class and one after the last class, each with a frequency of 0. The class width is 10.
- The imaginary class before 0-10 is -10 to 0, with class mark $\frac{-10+0}{2} = -5$. The point is (-5, 0).
- The imaginary class after 70-80 is 80-90, with class mark $\frac{80+90}{2} = 85$. The point is (85, 0).
4. Join the midpoints plotted in step 2 with line segments, starting from the point (-5, 0) and ending at the point (85, 0).
The resulting line graph is the frequency polygon.
Note: You can draw the frequency polygon without the histogram by directly plotting the points (class mark, frequency) and connecting them, including the points for the imaginary classes at the beginning and end.
Question 28. Prove that two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle.
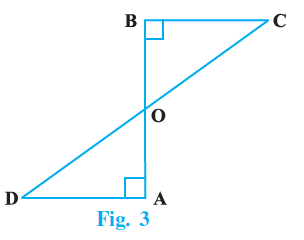
Using above, prove that CD bisects AB, in Figure 3, where AD and BC are equal perpendiculars to line segment AB.
Answer:
Part 1: Proof of ASA Congruence Criterion
Theorem: Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle (ASA criterion).
Given:
Two triangles $\triangle ABC$ and $\triangle DEF$ such that:
$\angle B = \angle E$
$\angle C = \angle F$
$BC = EF$
To Prove:
$\triangle ABC \cong \triangle DEF$
Proof:
We consider three cases for the length of side AB compared to side DE.
Case 1: Assume AB = DE.
In $\triangle ABC$ and $\triangle DEF$, we have:
$AB = DE$
(Assumed)
$\angle B = \angle E$
(Given)
$BC = EF$
(Given)
By the **SAS congruence criterion** (Side-Angle-Side), $\triangle ABC \cong \triangle DEF$.
Case 2: Assume AB > DE.
Choose a point P on AB such that PB = DE. Join PC.
Consider $\triangle PBC$ and $\triangle DEF$. We have:
$PB = DE$
(By construction)
$\angle B = \angle E$
(Given)
$BC = EF$
(Given)
By the SAS congruence criterion, $\triangle PBC \cong \triangle DEF$.
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), $\angle PCB = \angle DFE$.
However, we are given that $\angle ACB = \angle DFE$.
Therefore, $\angle PCB = \angle ACB$.
This is only possible if point P coincides with point A (since C is not on the line AB and $\angle ACB \neq 0$).
If P coincides with A, then AB = PB. But by construction, PB = DE. So, AB = DE.
This contradicts our assumption that AB > DE. Thus, the assumption AB > DE is false.
Case 3: Assume AB < DE.
Choose a point Q on DE such that QE = AB. Join QF.
Consider $\triangle ABC$ and $\triangle QEF$. We have:
$AB = QE$
(By construction)
$\angle B = \angle E$
(Given)
$BC = EF$
(Given)
By the SAS congruence criterion, $\triangle ABC \cong \triangle QEF$.
By CPCTC, $\angle BCA = \angle EFQ$.
However, we are given that $\angle BCA = \angle EFD$.
Therefore, $\angle EFQ = \angle EFD$.
This is only possible if point Q coincides with point D (since F is not on the line DE and $\angle EFD \neq 0$).
If Q coincides with D, then DE = QE. But by construction, QE = AB. So, DE = AB.
This contradicts our assumption that AB < DE. Thus, the assumption AB < DE is false.
From the three cases, the only possibility is AB = DE.
When AB = DE, we proved in Case 1 that $\triangle ABC \cong \triangle DEF$ by SAS.
Hence, the ASA congruence criterion is proved: if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle, the triangles are congruent.
Part 2: Proof that CD bisects AB using ASA Criterion
Given:
In Figure 3, AD $\perp$ AB, BC $\perp$ AB, and AD = BC. CD intersects AB at O.
To Prove:
CD bisects AB (i.e., AO = OB).
Proof:
Since AD is perpendicular to the line segment AB, the angle $\angle DAB$ is $90^\circ$.
$\angle DAB = 90^\circ$
(Given AD $\perp$ AB)
Since BC is perpendicular to the line segment AB, the angle $\angle CBA$ is $90^\circ$.
$\angle CBA = 90^\circ$
(Given BC $\perp$ AB)
From the figure, $\angle DAO$ is the same as $\angle DAB$ and $\angle CBO$ is the same as $\angle CBA$.
$\angle DAO = \angle CBO = 90^\circ$
... (i)
Since both line segments AD and BC are perpendicular to the same line segment AB, they are parallel to each other.
$AD \ || \ BC$
(Lines perpendicular to the same line are parallel)
Consider CD as a transversal intersecting the parallel lines AD and BC. The alternate interior angles formed are equal.
$\angle ADO = \angle BCO$
(Alternate interior angles)
Now, consider the triangles $\triangle$AOD and $\triangle$BOC.
We have the following equal parts:
$\angle DAO = \angle CBO$
[From (i)]
$AD = BC$
(Given)
$\angle ADO = \angle BCO$
[Proved above]
In $\triangle AOD$, we have an angle ($\angle DAO$), the included side (AD), and another angle ($\angle ADO$). Similarly, in $\triangle BOC$, we have an angle ($\angle CBO$), the included side (BC), and another angle ($\angle BCO$).
Since $\angle DAO = \angle CBO$, AD = BC, and $\angle ADO = \angle BCO$, by the **ASA congruence criterion** proved in Part 1, the triangles $\triangle AOD$ and $\triangle BOC$ are congruent.
$\triangle AOD \cong \triangle BOC$
(By ASA congruence criterion)
Since the triangles are congruent, their corresponding parts are equal by CPCTC.
Therefore, the corresponding sides AO and BO are equal.
$AO = BO$
(CPCTC)
Also, the corresponding sides DO and CO are equal.
$DO = CO$
(CPCTC)
The fact that AO = BO means that the point O is the midpoint of the line segment AB.
Since CD passes through O, where O is the midpoint of AB, the line segment CD bisects the line segment AB.
Hence Proved.
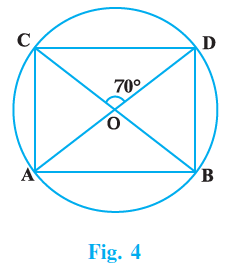
Question 29. Prove that equal chords AB and CD of a circle subtend equal angles at the centre. Use the above to find ABO in Figure 4, where O is the centre of the circle
Answer:
Part 1: Proof that Equal Chords Subtend Equal Angles at the Centre
Theorem: Equal chords of a circle subtend equal angles at the centre.
Given:
A circle with centre O.
Two equal chords AB and CD, i.e., AB = CD.
To Prove:
The angle subtended by chord AB at the centre ($\angle AOB$) is equal to the angle subtended by chord CD at the centre ($\angle COD$).
$\angle AOB = \angle COD$
Proof:
Consider the triangles $\triangle$AOB and $\triangle$COD.
OA and OB are radii of the circle with centre O.
OC and OD are radii of the same circle.
OA = OC
(Radii of the same circle)
OB = OD
(Radii of the same circle)
We are given that the chords are equal.
AB = CD
(Given)
In $\triangle$AOB and $\triangle$COD, we have:
OA = OC
(Side)
OB = OD
(Side)
AB = CD
(Side)
By the **SSS congruence criterion** (Side-Side-Side), the triangles $\triangle$AOB and $\triangle$COD are congruent.
$\triangle AOB \cong \triangle COD$
(By SSS congruence criterion)
Since the triangles are congruent, their corresponding parts are equal by CPCTC.
Therefore, the angle subtended by chord AB at the centre ($\angle AOB$) is equal to the angle subtended by chord CD at the centre ($\angle COD$).
$\angle AOB = \angle COD$
(CPCTC)
Hence Proved.
Part 2: Finding $\angle ABO$ in Figure 4
Given:
In Figure 4, O is the centre of the circle.
AB and CD are equal chords.
$\angle COD = 60^\circ$ (From the figure, or implied by context/question if not explicitly stated).
To Find:
The measure of $\angle ABO$.
Solution:
From Part 1, we proved that equal chords subtend equal angles at the centre.
Since AB = CD, the angle subtended by AB at the centre is equal to the angle subtended by CD at the centre.
$\angle AOB = \angle COD$
Given $\angle COD = 60^\circ$,
$\angle AOB = 60^\circ$
Now consider $\triangle$AOB.
OA and OB are radii of the same circle.
OA = OB
(Radii)
Since two sides of $\triangle$AOB are equal, it is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are equal.
$\angle OAB = \angle OBA$
(Angles opposite to equal sides OA and OB)
Let $\angle OAB = \angle OBA = x$. The angle $\angle OBA$ is the same as $\angle ABO$.
The sum of angles in a triangle is $180^\circ$. In $\triangle$AOB:
$\angle OAB + \angle OBA + \angle AOB = 180^\circ$
(Angle sum property of a triangle)
Substitute the known values:
$x + x + 60^\circ = 180^\circ$
$2x + 60^\circ = 180^\circ$
Solve for $x$:
$2x = 180^\circ - 60^\circ$
$2x = 120^\circ$
$x = \frac{120^\circ}{2}$
$x = 60^\circ$
Since $\angle ABO = x$, we have $\angle ABO = 60^\circ$.
Note that in $\triangle$AOB, since all angles are $60^\circ$, it is an equilateral triangle, which implies AB = OA = OB. This is consistent with the chords being equal and subtending a 60-degree angle at the center.
The measure of $\angle ABO$ is $60^\circ$.
Question 30. Factorise the expression
8x3 + 27 y3 + 36x2 y + 54xy2
OR
The Linear equation that converts Fahrenheit to Celsius is F = $\frac{9}{5}$ C + 32
Draw the graph of the equation using Celsius for x-axis and Fahrenheit for y-axis.
From the graph find the temperature in Fahrenheit for a temprature of 30°C.
Answer:
Given Expression:
$8x^3 + 27y^3 + 36x^2y + 54xy^2$
To Factorise:
Factorise the given expression.
Solution:
We examine the given expression $8x^3 + 27y^3 + 36x^2y + 54xy^2$.
We can observe that the first two terms are perfect cubes:
$8x^3 = (2x)^3$
$27y^3 = (3y)^3$
Let's consider the identity for the cube of a binomial sum:
$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$
... (i)
Let's see if the given expression fits this form with $a = 2x$ and $b = 3y$.
The terms $a^3$ and $b^3$ match $(2x)^3$ and $(3y)^3$.
Now, let's check the middle terms $3a^2b$ and $3ab^2$ with $a=2x$ and $b=3y$:
$3a^2b = 3(2x)^2(3y)$
$3a^2b = 3(4x^2)(3y)$
$3a^2b = 36x^2y$
This matches the third term in the given expression.
$3ab^2 = 3(2x)(3y)^2$
$3ab^2 = 3(2x)(9y^2)$
$3ab^2 = 54xy^2$
This matches the fourth term in the given expression.
Since all the terms match the expansion of $(2x + 3y)^3$, we can factorise the given expression as $(2x + 3y)^3$.
$8x^3 + 27y^3 + 36x^2y + 54xy^2 = (2x)^3 + 3(2x)^2(3y) + 3(2x)(3y)^2 + (3y)^3$
$= (2x + 3y)^3$
The factorised expression is $(2x + 3y)^3$.

